Sketch of The Analytical Engine
Augusta Ada, Countess of Lovelace はヴィクトリア朝時代の英国の女性で世界最初のプログラマであると考えられています。この文書は L. F. Menabrea というイタリア軍技官 (後のイタリア首相) が Charles Babbage が考案した解析機関を紹介するために書いた論文を Ada が翻訳したものです。Ada は翻訳にあたり、A 〜 G のタイトルがふられたノートを補遺として追加しました。Note G には解析機関を使用してベルヌーイ数を計算する方法が書かれています。
Ada の計算機科学への貢献については様々な議論があります。Brian Randall は "The Origin of Digital Computer" の中で、ベルヌーイ数計算プログラムは、最初 Babbage が Ada の協力により書き下ろしたと主張しています。Note G は Ada と Babbage の間でなんどもやり取りされました。Babbage がサポートしていたのは間違いないのですが、始終 Ada 主導で執筆が進められたようです。Ada は Babbage の致命的なミスも指摘しています (Joan Baum、Calculating Passion of Ada Byron)
Ada の翻訳と Note は 1843 年 9月、Richard Taylor が発行する Scientific Memoirs に掲載されました。Ada の希望により翻訳者は匿名扱いで A.A.L とだけ書かれました。
ここでは Ada が英訳した本文の対訳を掲載します。今となっては Note に比べて興味を引く内容ではないのですが、なぜ早くて正確な計算機が必要とされたのかといった時代背景を知るには良い読み物だと思います。また本文には Ada の訳注がついているのですが含めていません。時間があれば追加したいと思います。
Invented by Charles Babbage
By L. F. MENABREA of Turin, Officer of the Military Engineers
from the Bibliotheque Universelle de Geneve, October, 1842, No. 82
With notes upon the Memoir by the Translator ADA AUGUSTA, COUNTESS OF LOVELACE
Those labours which belong to the various branches of the mathematical sciences, although on first consideration they seem to be the exclusive province of intellect, may, nevertheless, be divided into two distinct sections;one of which may be called the mechanical, because it is subjected to precise and invariable laws, that are capable of being expressed by means of the operations of matter;while the other, demanding the intervention of reasoning, belongs more specially to the domain of the understanding. This admitted, we may propose to execute, by means of machinery, the mechanical branch of these labours, reserving for pure intellect that which depends on the reasoning faculties. Thus the rigid exactness of those laws which regulate numerical calculations must frequently have suggested the employment of material instruments, either for executing the whole of such calculations or for abridging them;and thence have arisen several inventions having this object in view, but which have in general but partially attained it. For instance, the much-admired machine of Pascal is now simply an object of curiosity, which, whilst it displays the powerful intellect of its inventor, is yet of little utility in itself. Its powers extended no further than the execution of the first four operations of arithmetic, and indeed were in reality confined to that of the first two, since multiplication and division were the result of a series of additions and subtractions. The chief drawback hitherto on most of such machines is, that they require the continual intervention of a human agent to regulate their movements, and thence arises a source of errors;so that, if their use has not become general for large numerical calculations, it is because they have not in fact resolved the double problem which the question presents, that of correctness in the results, united with economy of time.
数学の様々な分野に属する作業は、それぞれがある専門的な知識に特化したものである。それでも大きく二つに分けることができるだろう。一つ目は機械的な作業によるもので、正確性と一定の法則に支配される分野。「計算」に関することと言うこともできる。もう一つは、推論を要求する分野。より限定的に言うと「考える」という領域に属する分野である。我々は、機械的な作業は機械的な手段によって遂行し、推論の能力に依存する、純粋な思考に注力すべきだろう。数値計算を規定する法則の厳密な正確性は、計算の全てもしくは一部を遂行するために、何らかの道具を使うことを、人々に度々思い起こさせたに違いない。そして、そこからいくつかの考案がなされた。それはある程度目的を達するものだったが、まだ不十分だった。例えば、大いに賞賛を浴びたパスカルの機械（パスカリーヌのことと思われる）は、今では単に好奇の対象でしかない。発明者の素晴らしい知性を証明するものではあっても、もはやそれはごく限られたことにしか使えない代物だ。その能力は四則演算を超えない。乗算と除算は加算と減算の組み合わせで実現していたので、実際は加算と減算の二種類しかできなかったのだ。今まで作られた、この手の機械のほとんどは、動作に秩序を持たせるために人の介入を必要とする欠点を持っている。そしてそれは誤りの原因となる。それが大きな数を計算する一般的な方法になっていないとすれば、正確性と時間の節約という密接に絡み合った問題を解決していないのが理由である。
Struck with similar reflections, Mr. Babbage has devoted some years to the realization of a gigantic idea. He proposed to himself nothing less than the construction of a machine capable of executing not merely arithmetical calculations, but even all those of analysis, if their laws are known. The imagination is at first astounded at the idea of such an undertaking;but the more calm reflection we bestow on it, the less impossible does success appear, and it is felt that it may depend on the discovery of some principle so general, that, if applied to machinery, the latter may be capable of mechanically translating the operations which may be indicated to it by algebraical notation. The illustrious inventor having been kind enough to communicate to me some of his views on this subject during a visit he made at Turin, I have, with his approbation, thrown together the impressions they have left on my mind. But the reader must not expect to find a description of Mr. Babbage's engine;the comprehension of this would entail studies of much length;and I shall endeavour merely to give an insight into the end proposed, and to develop the principles on which its attainment depends.
同様の考えを持ったバベッジ氏は、数年の歳月を途方もない考えの実現につぎ込んだ。彼は、少なくとも、算術計算だけではなく、法則を与えてやればあらゆる解析さえも実行できる機械を構築しようと心に決めた。最初は、そのような仕事を思いつくことに驚いた。しかし、落ち着いて良く考えてみると、不可能というほどのことではない。もし機械に適用するのであれば、それほど一般的ではないが、おそらくある種の原理を見つけられるかどうかにかかっているように思える。それができれば、代数表記によって表示されるであろう計算を機械的に解釈することができるだろう。この著名な考案者は、トリノに滞在している間、このことに関する彼の考えを親切に教えてくれた。また、私も彼の許しを得て、その考えによって私の心にもたらされた感想を述べた。
とはいえ、読者はバベッジ氏の機関についての説明を期待してはいけない。それを理解するには、もっと多くの学習が必要となる。ここでは、それが目標とするところに関する考察を与え、それを達成するために必要な原理を引き出すよう努めるだけだ。
I must first premise that this engine is entirely different from that of which there is a notice in the ‘Treatise on the Economy of Machinery,’ by the same author. But as the latter gave rise to the idea of the engine in question, I consider it will be a useful preliminary briefly to recall what were Mr. Babbage's first essays, and also the circumstances in which they originated.
まず最初に、同じ著者によって書かれた『機械の経済に関する論文（Treatise on the Economy of Machinery)』の中で論評された機関とは異なることを前提としなければいけない。とはいえ、解析機関とは何かという問いに先立ち、バベッジ氏の初期の試みが何であったか、またそれらの元となった諸条件は何かということを簡単に思い返すのは有用だと考える。
It is well known that the French government, wishing to promote the extension of the decimal system, had ordered the construction of logarithmical and trigonometrical tables of enormous extent. M. de Prony, who had been entrusted with the direction of this undertaking, divided it into three sections, to each of which was appointed a special class of persons. In the first section the formula were so combined as to render them subservient to the purposes of numerical calculation;in the second, these same formula were calculated for values of the variable, selected at certain successive distances;and under the third section, comprising about eighty individuals, who were most of them only acquainted with the first two rules of arithmetic, the values which were intermediate to those calculated by the second section were interpolated by means of simple additions and subtractions.
十進数の範囲拡張を促進することを望み、フランス政府が対数と三角関数の巨大な表を作るよう命じたことはよく知られている。この仕事を指揮するよう任命されたデプロニは、それを三つのセクションに分け、それぞれを特別な階層の人々に割り振った。最初のセクションでは、いくつかの公式が数値計算に適するように結合された。二番目のセクションでは、これらの等価公式を用いて変数の値が計算された。これにはある特定の連続した範囲が選ばれた。そして、三番目のセクションは大体八十人の個人からなり、そのほとんどが二つの算術規則しか習熟していなかった。二番目のセクションで計算された値が彼らに伝えられ、足し算と引き算を行うことにより値が補間された。
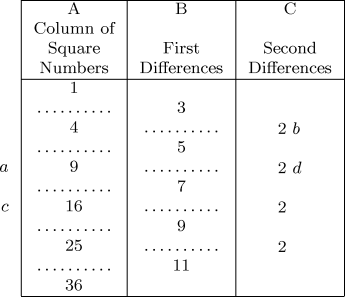
An undertaking similar to that just mentioned having been entered upon in England, Mr. Babbage conceived that the operations performed under the third section might be executed by a machine;and this idea he realized by means of mechanism, which has been in part put together, and to which the name Difference Engine is applicable, on account of the principle upon which its construction is founded. To give some notion of this, it will suffice to consider the series of whole square numbers, 1, 4, 9, 16, 25, 36, 49, 64, &c. By subtracting each of these from the succeeding one, we obtain a new series, which we will name the Series of First Differences, consisting of the numbers 3, 5, 7, 9, 11, 13, 15, &c. On subtracting from each of these the preceding one, we obtain the Second Differences, which are all constant and equal to 2. We may represent this succession of operations, and their results, in the following table.
イングランドで、ちょうどそれと似たような作業が開始されていて、バベッジ氏は上記の第三セクションの作業は機械で実行できるかもしれないと考えた。彼はこのアイデアをある程度まとまった機械的方法により実現した。そしてそれはその構造の基本となる原理を考慮して、階差機関（Difference Engine）という名前が適している。この考えを具体的に示すには、全て平方数の数列 1、4、9、16、25、36、49、64、…… を考えればよい。各々を後ろの数字から引くことによって、3、5、7、9、11、13、15、…… という新しい数列を得る。これを最初の階差数列（First Differences Series）と呼ぶことにする。さらに、引くと、第二階差（Second Differences）を得る。そして、それはすべて定数 2 となる。ここで、この一連の計算とその結果を次表に示す。※ series は級数の意味だがここでは数列と訳する。
From the mode in which the last two columns B and C have been formed, it is easy to see, that if, for instance, we desire to pass from the number 5 to the succeeding one 7, we must add to the former the constant difference 2;similarly, if from the square number 9 we would pass to the following one 16, we must add to the former the difference 7, which difference is in other words the preceding difference 5, plus the constant difference 2;or again, which comes to the same thing, to obtain 16 we have only to add together the three numbers 2, 5, 9, placed obliquely in the direction ab. Similarly, we obtain the number 25 by summing up the three numbers placed in the oblique direction dc: commencing by the addition 2+7, we have the first difference 9 consecutively to 7;adding 16 to the 9 we have the square 25. We see then that the three numbers 2, 5, 9 being given, the whole series of successive square numbers, and that of their first differences likewise may be obtained by means of simple additions.
B と C の列の構成方法から、例えば B 列において数字 5 から次の 7 に至るには、先の定数 2 を加えなければいけないことは容易に分かる。同様に平方数 9 から次の 16 に至るとすると、B 列の差 7 を加えなければいけない。これは、B 列における差 7 の一つ前の数字 5 に定数 2 を加えたものとも言える。同じことを繰り返すが、16 を得るためには、表で記号 a から b へ斜めに並んだ三つの数字、2、5、9 を足し合わせるだけでよい。同様に、記号 d から c に斜めに並んだ三つの数字を合計することによって平方数 25 を得る。2 + 7 から開始すると、最初の差 9 を 7 から連続した数として得る。そして、16 を 9 に加えると、平方数 25 を得る。最初の三つの数 2、5、9 が与えられれば、連続した全ての平方数と最初の差は、単純な足し算によって同様に得られるだろう。
Now, to conceive how these operations may be reproduced by a machine, suppose the latter to have three dials, designated as A, B, C, on each of which are traced, say a thousand divisions, by way of example, over which a needle shall pass. The two dials, C, B, shall have in addition a registering hammer, which is to give a number of strokes equal to that of the divisions indicated by the needle. For each stroke of the registering hammer of the dial C, the needle B shall advance one division;similarly, the needle A shall advance one division for every stroke of the registering hammer of the dial B. Such is the general disposition of the mechanism.
さて、このような計算をどのようにして機械で実現できるかを考えるため、A、B、C と指定された三つのダイヤルを持っている装置を考える。それぞれは千分の一まで目盛りを読むことが出来る。例えば、針がついていて目盛りの上を動くようにできているとする。加えて、二つのダイヤル C、B には記録ハンマーがついていて、針が示す目盛りと同じ数だけ動く。ダイヤル C の記録ハンマーが動く度に、ダイヤル B のメモリは一つ進む。同様に、ダイヤル B の記録ハンマーが動く度に A の針は一つ進む。このような動作が想定する装置の大雑把な機構である。
This being understood, let us, at the beginning of the series of operations we wish to execute, place the needle C on the division 2, the needle B on the division 5, and the needle A on the division 9. Let us allow the hammer of the dial C to strike;it will strike twice, and at the same time the needle B will pass over two divisions. The latter will then indicate the number 7, which succeeds the number 5 in the column of first differences. If we now permit the hammer of the dial B to strike in its turn, it will strike seven times, during which the needle A will advance seven divisions;these added to the nine already marked by it will give the number 16, which is the square number consecutive to 9. If we now recommence these operations, beginning with the needle C, which is always to be left on the division 2, we shall perceive that by repeating them indefinitely, we may successively reproduce the series of whole square numbers by means of a very simple mechanism.
この仕組みは段々と分かるだろう。我々が実行したいと考えている一連の計算の始めに、まず C の針を 2、B の針を 5、A の針を 9 に合わせる。ダイヤル C のハンマーを動かすと二回打つことになる。そして、針 B は二目盛り進み、7 を指し示す。これは前の表の最初の階差の列 5 に 2 が加えられたものだ。そして、ダイヤル B のハンマーを動かすと七回打ち、針 A は七目盛り進む。最初に示していた 9 に加えられるので、目盛りは 16 となる。これは 9 の次の平方数だ。この操作を針 C から繰り返すとする。C は常に 2 を示しているので、これを無限に繰り返すことにより、簡単な方法で平方数を連続して作り出すことができることに気付くだろう。
The theorem on which is based the construction of the machine we have just been describing, is a particular case of the following more general theorem: that if in any polynomial whatever, the highest power of whose variable is m, this same variable be increased by equal degrees;the corresponding values of the polynomial then calculated, and the first, second, third, &c. differences of these be taken (as for the preceding series of squares);the mth differences will all be equal to each other. So that, in order to reproduce the series of values of the polynomial by means of a machine analogous to the one above described, it is sufficient that there be (m+1) dials, having the mutual relations we have indicated. As the differences may be either positive or negative, the machine will have a contrivance for either advancing or retrograding each needle, according as the number to be algebraically added may have the sign plus or minus.
このようなこの機械の基礎となる原理は、より一般的な原理のある特殊な場合である。どのような多項式でも、もっとも高次の変数の指数を m とすると、この変数は同じだけ増加される。そして、それに対する多項式の値が計算される。そして、最初の値、二番目、三番目といった具合に、それらの階差が計算されていく（先の平方数のように）m 番目の階差は全て同じ数になる。従って、先に示したのと同じような機械によって多項式の一連の値を計算するには、相互関係も先に示したのと同じ (m+1) 個のダイヤルがあれば良いことになる。階差は正と負どちらの値でも良く、代数的に加算される数が正と負の符号を持ち得るのに対応して、機械は針を前進もしくは後退する仕組みを持つ。
If from a polynomial we pass to a series having an infinite number of terms, arranged according to the ascending powers of the variable, it would at first appear, that in order to apply the machine to the calculation of the function represented by such a series, the mechanism must include an infinite number of dials, which would in fact render the thing impossible. But in many cases the difficulty will disappear, if we observe that for a great number of functions the series which represent them may be rendered convergent;so that, according to the degree of approximation desired, we may limit ourselves to the calculation of a certain number of terms of the series, neglecting the rest. By this method the question is reduced to the primitive case of a finite polynomial. It is thus that we can calculate the succession of the logarithms of numbers. But since, in this particular instance, the terms which had been originally neglected receive increments in a ratio so continually increasing for equal increments of the variable, that the degree of approximation required would ultimately be affected, it is necessary, at certain intervals, to calculate the value of the function by different methods, and then respectively to use the results thus obtained, as data whence to deduce, by means of the machine, the other intermediate values. We see that the machine here performs the office of the third section of calculators mentioned in describing the tables computed by order of the French government, and that the end originally proposed is thus fulfilled by it.
多項式から無理数項を持つ級数（series）に移行し、増え続ける変数の次数に対応するとする。そのような級数によって表現される関数の計算に機械を適用するためには、無限の数のダイヤルを持つ構造にならざるを得ない。これは、物事を事実上不可能にするかのように見える。しかし、多くの場合困難は消える。そのようにして表現される数多くの関数を調べてみると、それらは収束するものへ変えることができる。そのため、要求する近似の度合いによって、計算する級数の項数に制限を設け、残りの項は無視することができる。この方法によって、問題が有限多項式の基本的な場合に単純化される。それは、このように、我々が綿々とした対数の値を計算することができるということだ。しかし、この特定の例においては、元々無視されてきた項の占める割合が、変数増分と同じだけ連続して増え続け、最終的には要求する近似の度合いに影響を与える。ある間隔で、違った方法により関数の値を計算し、機械により他の中間値を推定することにより得られた結果と、それぞれに使う必要がある。 フランス政府の命令により計算された表ついて言及した際の第三のセクションの計算手たちの役割を、ここに機械が果たすことができることが分かる。そして、それはそもそも掲げていた到達点も満足するのだ。
Such is the nature of the first machine which Mr. Babbage conceived. We see that its use is confined to cases where the numbers required are such as can be obtained by means of simple additions or subtractions;that the machine is, so to speak, merely the expression of one particular theorem of analysis;and that, in short, its operations cannot be extended so as to embrace the solution of an infinity of other questions included within the domain of mathematical analysis. It was while contemplating the vast field which yet remained to be traversed, that Mr. Babbage, renouncing his original essays, conceived the plan of another system of mechanism whose operations should themselves possess all the generality of algebraical notation, and which, on this account, he denominates the Analytical Engine.
これは、バベッジ氏が最初に考えたこの機械の性質だ。その使用は、要求される数字がそのような単純な足し算と引き算により得られる場合に限られることが分かる。つまりこのこの機械は、ある特定の解析の原理を表現しただけのものと言える。要するに、その動作は他に無限にある数学的解析分野に含まれる問題の解法を包含するところまで拡張することはできない。まだ縦断されていない広大なフィールドについて考慮していた時、バベッジ氏は元の企てを放棄して、全ての一般的な代数的な表現を包含するはずであろう動作を持つもう一つのシステム構造の計画を思いついた。そして、彼は、そのような性質から、それを解析機関（Analytical Engine）と命名した。
Having now explained the state of the question, it is time for me to develop the principle on which is based the construction of this latter machine. When analysis is employed for the solution of any problem, there are usually two classes of operations to execute:first, the numerical calculation of the various coefficients;and secondly, their distribution in relation to the quantities affected by them. If, for example, we have to obtain the product of two binomials (a+bx) (m+nx), the result will be represented by am + (an + bm) x + bnx2, in which expression we must first calculate am, an, bm, bn;then take the sum of an + bm;and lastly, respectively distribute the coefficients thus obtained amongst the powers of the variable. In order to reproduce these operations by means of a machine, the latter must therefore possess two distinct sets of powers:first, that of executing numerical calculations;secondly, that of rightly distributing the values so obtained.
問題の状況が説明されたので、このこの機械の仕組みの基礎となる原理を考えることとする。あらゆる問題の解法として使用され、通常実行されるのは二種類の演算である。最初は様々な係数の数値計算、その次は、それに影響される量と関連した、係数の配分だ。例えば、二つの二項式 (a+bx) (m+nx) の積を考えると、その結果は am +（an + bm)x + bnx2 と表現される。この式では、最初に am、an、bm、bn を計算しなければいけない。それから an + bm を計算する。最後に、そのようにして得られた係数を、それぞれの次数の変数に配分する。機械によりこれらの演算を実現するには、この機械は二組の異なる能力を持っていなければいけない。まず数値計算を実行する能力、そして、得られた値を正しく配分する能力である。
But if human intervention were necessary for directing each of these partial operations, nothing would be gained under the heads of correctness and economy of time;the machine must therefore have the additional requisite of executing by itself all the successive operations required for the solution of a problem proposed to it, when once the primitive numerical data for this same problem have been introduced. Therefore, since, from the moment that the nature of the calculation to be executed or of the problem to be resolved have been indicated to it, the machine is, by its own intrinsic power, of itself to go through all the intermediate operations which lead to the proposed result, it must exclude all methods of trial and guess-work, and can only admit the direct processes of calculation.
しかし、部分的な演算の度に人の介入が必要なのであれば、正確性と時間の節約を期するという点では得る物がない。従って、一度この同じ問題のための基本的な数値データが入力されたなら、この機械（the machine）は与えられた問題を解くために、必要となる一連の演算全てを自身でこなす能力を持たなければいけない。つまり、実行されるべき計算や解かれるべき問題が提示された瞬間から、本質的な能力で、与えられた結果に至るまでの中間的な演算全てを行う。一直線な計算過程のみを許容するので、あらゆる試行錯誤は除外されなければいけない。
It is necessarily thus;for the machine is not a thinking being, but simply an automaton which acts according to the laws imposed upon it. This being fundamental, one of the earliest researches its author had to undertake, was that of finding means for effecting the division of one number by another without using the method of guessing indicated by the usual rules of arithmetic. The difficulties of effecting this combination were far from being among the least;but upon it depended the success of every other. Under the impossibility of my here explaining the process through which this end is attained, we must limit ourselves to admitting that the first four operations of arithmetic, that is addition, subtraction, multiplication and division, can be performed in a direct manner through the intervention of the machine. This granted, the machine is thence capable of performing every species of numerical calculation, for all such calculations ultimately resolve themselves into the four operations we have just named. To conceive how the machine can now go through its functions according to the laws laid down, we will begin by giving an idea of the manner in which it materially represents numbers.
これは必然的なことだ。この機械は思考力を持つ存在ではなく、それに与えられた規則に従って動く単純な自動装置である。これは基本的な原理で、機械の作者が取り組まなければいけない初期の研究のうちのひとつは、通常の計算規則により提示される思考方法によらずに、ある数字を別の数字で割るということに意味を持たせる方法を見つけることだった。この組み合わせに意味を持たせる困難は決して少ないものではない。そして、あらゆる他の成功に依存するものだった。ここに私が説明した、目的を達成する過程の不可能性の下では、四則演算のみを扱うところに妥協しなければいけない。つまり、加算、減算、乗算、そして除算である。これらの演算は直接機械内部で実行することができる。これにより、この機械は、あらゆる種類の数値計算、つまり指定した四つの演算に分解できる計算全てを、実行することができるようになる。この機械が、設定された規則に従いその機能を実行する方法を考えるために、数を具現する形式に関するアイデアから始めることにする。
Let us conceive a pile or vertical column consisting of an indefinite number of circular discs, all pierced through their centres by a common axis, around which each of them can take an independent rotatory movement. If round the edge of each of these discs are written the ten figures which constitute our numerical alphabet, we may then, by arranging a series of these figures in the same vertical line, express in this manner any number whatever. It is sufficient for this purpose that the first disc represent units, the second tens, the third hundreds, and so on. When two numbers have been thus written on two distinct columns, we may propose to combine them arithmetically with each other, and to obtain the result on a third column. In general, if we have a series of columns consisting of discs, which columns we will designate as V0V1, V2, V3, V4, &c., we may require, for instance, to divide the number written on the column V1 by that on the column V4, and to obtain the result on the column V7. To effect this operation, we must impart to the machine two distinct arrangements;through the first it is prepared for executing a division, and through the second the columns it is to operate on are indicated to it, and also the column on which the result is to be represented. If this division is to be followed, for example, by the addition of two numbers taken on other columns, the two original arrangements of the machine must be simultaneously altered. If, on the contrary, a series of operations of the same nature is to be gone through, then the first of the original arrangements will remain, and the second alone must be altered Therefore, the arrangements that may be communicated to the various parts of the machine may be distinguished into two principal classes:
不明確な数の円盤を積み重ねた物や垂直の円柱を考える。全ての円盤は中心軸を通る穴が空けられており、それぞれは独立してその軸を中心に回転することができる。それぞれの円盤の外周に、数字化されたアルファベットからなる十の数字が書かれとすると、その数字の連なりを同じ垂直の列で揃えることにより、どのような数字も表現できるだろう。最初の円盤は一の位、二番目の円盤は十の位、三番目の円盤は百の位といった具合にやれば、この目的を達せられる。二つの数字を異なる円柱に書けば、その数字同士を算術的に組み合わせ、もうひとつの円柱に結果を出すように命じることができるだろう。一般に、円盤からなる円柱を連ね、それぞれを V0、V1、V2、V3、V4、…… と呼ぶことにする。我々は、例えば、円柱 V1 に書かれた数字を V4 で割り、結果を V7 に出すという風に命じることができるだろう。この演算に意味を持たせるためには、二つの準備を行わなければいけない。最初は、機械が除算を実行するための準備、次に、演算が行われる円柱の指定である。結果が表示される円柱も指定される。もしこの除算に続いて、例えば、別の円柱による二つの数字の加算が行われるのであれば、最初に述べた二つの準備は一斉に変更されなければいけない。対照的に、同じ性質を持った一連の演算が行われているのであれば、最初の準備はそのままで、二番目の準備だけが変更されなければいけない。従って、この機械の様々な部分に伝えられるであろう準備は、二つの基本的な組に分けることができる。
By this latter we mean that which indicates the columns to be operated on. As for the operations themselves, they are executed by a special apparatus, which is designated by the name of mill, and which itself contains a certain number of columns, similar to those of the Variables. When two numbers are to be combined together, the machine commences by effacing them from the columns where they are written, that is, it places zero on every disc of the two vertical lines on which the numbers were represented;and it transfers the numbers to the mill. There, the apparatus having been disposed suitably for the required operation, this latter is effected, and, when completed, the result itself is transferred to the column of Variables which shall have been indicated. Thus the mill is that portion of the machine which works, and the columns of Variables constitute that where the results are represented and arranged. After the preceding explanations, we may perceive that all fractional and irrational results will be represented in decimal fractions. Supposing each column to have forty discs, this extension will be sufficient for all degrees of approximation generally required.
二番目の準備によって、我々は演算が行われる円柱を指示する。演算そのものに関しては、ミル（mill）と呼ばれる特別な装置によって実行される。ミルには、特定の数の変数と似たような円柱がある。二つの数字が組み合わされると、この機械はその数を消すことがから始める。つまり、両ディスクの数字が表示される垂直の列をゼロにする。それによって数字はミルへ送られる。そこでは、装置が要求された演算用のために適切に配置されていて、計算が実行される。そしてそれが終わると、結果は指定された変数の円柱に送られる。ミルはこの機械の一部として稼働するものであり、変数の円柱は結果が表示され用意される部分を構成するものだ。以降の説明により、全ての分数と無理数の結果は十進数の小数として表現されることが分かるだろう。それぞれの円柱が四十枚の円盤を持っていれば、一般に要求される近似の程度全てを満たすだろう。
It will now be inquired how the machine can of itself, and without having recourse to the hand of man, assume the successive dispositions suited to the operations. The solution of this problem has been taken from Jacquard's apparatus, used for the manufacture of brocaded stuffs, in the following manner:—
それでは、この機械はどのようにして、人の手を頼ることなく連続した演算に適応できるのだろうか。この問題の解法はジャカードの装置から得られた。それは模様織（brocaded stuffs）の生産に使われる装置で次のように動作する。
Two species of threads are usually distinguished in woven stuffs;one is the warp or longitudinal thread, the other the woof or transverse thread, which is conveyed by the instrument called the shuttle, and which crosses the longitudinal thread or warp. When a brocaded stuff is required, it is necessary in turn to prevent certain threads from crossing the woof, and this according to a succession which is determined by the nature of the design that is to be reproduced. Formerly this process was lengthy and difficult, and it was requisite that the workman, by attending to the design which he was to copy, should himself regulate the movements the threads were to take. Thence arose the high price of this description of stuffs, especially if threads of various colours entered into the fabric. To simplify this manufacture, Jacquard devised the plan of connecting each group of threads that were to act together, with a distinct lever belonging exclusively to that group. All these levers terminate in rods, which are united together in one bundle, having usually the form of a parallelopiped with a rectangular base. The rods are cylindrical, and are separated from each other by small intervals. The process of raising the threads is thus resolved into that of moving these various lever-arms in the requisite order. To effect this, a rectangular sheet of pasteboard is taken, somewhat larger in size than a section of the bundle of lever-arms. If this sheet be applied to the base of the bundle, and an advancing motion be then communicated to the pasteboard, this latter will move with it all the rods of the bundle, and consequently the threads that are connected with each of them. But if the pasteboard, instead of being plain, were pierced with holes corresponding to the extremities of the levers which meet it, then, since each of the levers would pass through the pasteboard during the motion of the latter, they would all remain in their places. We thus see that it is easy so to determine the position of the holes in the pasteboard, that, at any given moment, there shall be a certain number of levers, and consequently of parcels of threads, raised, while the rest remain where they were. Supposing this process is successively repeated according to a law indicated by the pattern to be executed, we perceive that this pattern may be reproduced on the stuff. For this purpose we need merely compose a series of cards according to the law required, and arrange them in suitable order one after the other; then, by causing them to pass over a polygonal beam which is so connected as to turn a new face for every stroke of the shuttle, which face shall then be impelled parallelly to itself against the bundle of lever-arms, the operation of raising the threads will be regularly performed. Thus we see that brocaded tissues may be manufactured with a precision and rapidity formerly difficult to obtain.
通常、二種類の糸が織物の中で区別されている。ひとつは縦糸である。もうひとつは横糸で、杼（shuttle）と呼ばれる器具によって、縦糸を横切って通される。模様織にする時には、特定の糸を横糸と交差させないことが必要だ。これは織ろうとしている模様により決まる連続した手順に従って行われる。かつてはこの過程は時間がかかり難しいもので、職人の技だった。再現しようとする模様に専心するには、糸を取る動きを制しなければいけなかった。そこからこの手の製品が高価になった。特にいろいろな色の糸が織り込まれたものは高い。この模様織の製造を単純化するために、ジャカードはそれぞれの糸の組が一緒に動くように、組にのみ属する別々のレバーに関連付ける方法を考案した。それぞれのレバーはロッドで終端している。そして、それは一束にまとめられられ、通常、長方形をベースとした平行六面体の形になる。ロッドは円筒形で、お互い小さな間隔を空けて離される。糸を持ち上げる過程は、これら数本のレバーを必要に応じて動かすことに分解される。これを動かすために、レバーアームの束の部分より幾分大きな長方形の厚紙が用いられる。この厚紙が束の底に置かれた、そして、前進する動きがそれに伝わったら、厚紙はそれによって全てのロッド束を動かし、その結果、それらと関連付けられた糸も動かす。しかし、厚紙が平坦ではなく、レバーの先端に合うように穴が開けられれていたら、それらのレバーは、厚紙が動いている間、それをやり過ごし、レバーは元の位置に残されたままになるだろう。従って、厚紙の穴の位置はそのように簡単に決定できることが分かる。どの瞬間においても、ある決まった数のレバー、それに伴う糸の一部が、それ以外の糸を置き去りにして、持ち上げられる。この過程が、織られる模様により示される規則に従って、連続して繰り返されると、模様が織物の上に再現されるというのが分かるだろう。この目的のために、要求される規則に従って一連のカードを作成し、それを適当な順序に配置するだけで良い。それから、糸を、杼が行き来する度に新しい面に変えるように接続された、多角形の梁の上を通らせることにより、面はそれ自身を平行に、レバーアームの束に対して押し進み、糸を持ち上げる操作は規則正しく行われる。こうして、かつては簡単ではなかった、模様付けされた織物が、正確かつ迅速に製造されるのが分かる。
Arrangements analogous to those just described have been introduced into the Analytical Engine. It contains two principal species of cards: first, Operation cards, by means of which the parts of the machine are so disposed as to execute any determinate series of operations, such as additions, subtractions, multiplications, and divisions;secondly, cards of the Variables, which indicate to the machine the columns on which the results are to be represented. The cards, when put in motion, successively arrange the various portions of the machine according to the nature of the processes that are to be effected, and the machine at the same time executes these processes by means of the various pieces of mechanism of which it is constituted.
これと類似した方法が解析機関に導入された。それには二種類の基本的なカードが使われる。一番目は演算カードで、これにより、加算、減算、乗算、除算といった、決められた一連の演算を実行するようこの機械の一部が準備される。二番目は、変数カードで、結果が表示されるカードを指定するもの。カードは、投入されると、実行される処理の性質に応じてこの機械の様々な部分を連続して準備する。そして、同時に、この機械は、その一部をなすさまざまな機構によりこれらの処理を実行する。
In order more perfectly to conceive the thing, let us select as an example the resolution of two equations of the first degree with two unknown quantities. Let the following be the two equations, in which x and y are the unknown quantities:—
より完全にこれを考えるために、二つの未知数を持つ連立一次方程式の解を例とする。次の x と y が未知数の二つの式を考える。
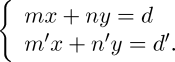
We deduce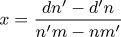 
, and for y an analogous expression. Let us continue to represent by V0, V1, V2, &c. the different columns which contain the numbers, and let us suppose that the first eight columns have been chosen for expressing on them the numbers represented by m, n, d, m', n', d', n and n', which implies that V0=m, V1=n, V2=d, V3=m', V4=n', V5=d', V6=n, V7=n'.
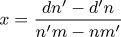が成り立つ。y も同様の式である。引き続き、違う番号を格納する円柱を V0、V1、V2、……と表現することとする。最初の八つの円柱は m、n、d、m'、n'、d'、n、n で表される数字を表現するために使われるものとする。つまり、V0=m、V1=n、V2=d、V3=m'、V4=n'、V5=d'、V6=n、V7=n' ということになる。
The series of operations commanded by the cards, and the results obtained, may be represented in the following table:—
カードにより指示される一連の計算と結果は次表のように表されるだろう。
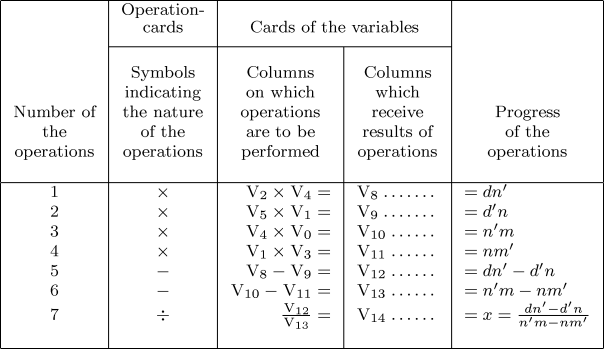
Since the cards do nothing but indicate in what manner and on what columns the machine shall act, it is clear that we must still, in every particular case, introduce the numerical data for the calculation. Thus, in the example we have selected, we must previously inscribe the numerical values of m, n, d, m', n', d', in the order and on the columns indicated, after which the machine when put in action will give the value of the unknown quantity x for this particular case. To obtain the value of y, another series of operations analogous to the preceding must be performed. But we see that they will be only four in number, since the denominator of the expression for y, excepting the sign, is the same as that for x, and equal to n'm-nm'. In the preceding table it will be remarked that the column for operations indicates four successive multiplications, two subtractions, and one division. Therefore, if desired, we need only use three operation-cards;to manage which, it is sufficient to introduce into the machine an apparatus which shall, after the first multiplication, for instance, retain the card which relates to this operation, and not allow it to advance so as to be replaced by another one, until after this same operation shall have been four times repeated. In the preceding example we have seen, that to find the value of x we must begin by writing the coefficients m, n, d, m', n', d', upon eight columns, thus repeating n and n' twice. According to the same method, if it were required to calculate y likewise, these coefficients must be written on twelve different columns. But it is possible to simplify this process, and thus to diminish the chances of errors, which chances are greater, the larger the number of the quantities that have to be inscribed previous to setting the machine in action. To understand this simplification, we must remember that every number written on a column must, in order to be arithmetically combined with another number, be effaced from the column on which it is, and transferred to the mill. Thus, in the example we have discussed, we will take the two coefficients m and n', which are each of them to enter into two different products, that is m into mn' and md', n' into mn' and n'd. These coefficients will be inscribed on the columns V0 and V4. If we commence the series of operations by the product of m into n', these numbers will be effaced from the columns V0 and V4, that they may be transferred to the mill, which will multiply them into each other, and will then command the machine to represent the result, say on the column V6. But as these numbers are each to be used again in another operation, they must again be inscribed somewhere;therefore, while the mill is working out their product, the machine will inscribe them anew on any two columns that may be indicated to it through the cards;and as, in the actual case, there is no reason why they should not resume their former places, we will suppose them again inscribed on V0 and V4, whence in short they would not finally disappear, to be reproduced no more, until they should have gone through all the combinations in which they might have to be used.
カードはどの円柱に対してどのように振る舞うかを指示するだけなので、全ての場合において、計算のための数値データを与えてやらなければいけないのは明らかである。我々が選んだ例では、事前に数値 m、n、d、m'、n'、d' を指定された円柱に順番通り書かなければいけなかった。その状態でこの機械が稼働すると、この場合の未知数 x が与えられた。y の値を求めるには、一連の演算を先の場合と同様に実行しなければいけない。しかし、それは四つの数字だけで良いのが分かる。分母の式は符号を除いて、x のものと同じである。つまり n'm-nm' となる。先の表では、円柱の計算は四つの連続した除算、二つの減算、そしてひとつの除算と指定されていることに気付くだろう。従って、三枚のカードだけを使うということもできる。これを実現するには、例えば、最初の除算の後、この演算に関するカードを保持し、これが四回繰り返されるまで、カードが次に進み差し変わるのを止める装置を導入すれば良い。この例では、未知数 x を算出するために、係数 m、n、d、m'、n'、d'、n、n を書き込むことから始めた。n と n' は二度書かれている。同じ方法でやると、y を求めるのに、このような係数を十二の円柱に書き込まなければいけないことになる。しかし、この処理を簡略化して、誤りが起きる可能性を減らすことができる。稼働前にこの機械にセットされる数値が多いほど、誤りの可能性が大きくなる。この簡略化を理解するためには、円柱上の数値は、算術的にもう一方の数値と組み合わせるために、円柱から消去しミルへ送らなければいけないことを思い起こす必要がある。先ほどの例では、二つの係数 m と n' を取り上げた。これらは、m は mn' と md' に、n' は mn' と n'd といった具合に、それぞれに違った積に入力される。これらの係数は円柱 V0 と V4 に書き込まれる。一連の演算を m と n' の積から始めるとすると、これらの数値は V0 と V4 から消去されミルに送られるだろう。そして、お互いに掛け合わされてこの機械に結果を表示するように命じることになる。V6 の円柱に書き込まれることにしよう。しかし、これらの番号はそれぞれに、別の演算で再利用される。どこかに書いておく必要がある。従って、ミルが積を処理した上で、さらにこの機械はそれらの数値を、カードによって指示されるであろう円柱に書くことになるのだ。そして、実際のケースでは、それらの数値は元にあった場所に書かれる理由はない。我々は、再び V0 と V4 に書かれると思うだろう。ようするに、結局は消されなかったことになるのだ。これ以上複写しないために、それらの数字が使われるであろう、全ての演算の組み合わせに供されるまでは。
We see, then, that the whole assemblage of operations requisite for resolving the two above equations of the first degree may be definitely represented in the following table:—
上記二つの一次方程式を解くために必要な全ての演算を寄せ集めると明らかに次の表のように表現されるはずだ（大きい画像）
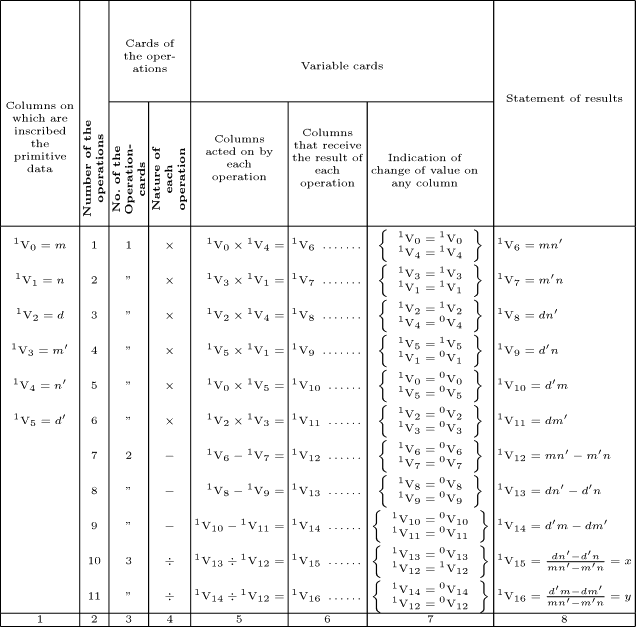
In order to diminish to the utmost the chances of error in inscribing the numerical data of the problem, they are successively placed on one of the columns of the mill;then, by means of cards arranged for this purpose, these same numbers are caused to arrange themselves on the requisite columns, without the operator having to give his attention to it; so that his undivided mind may be applied to the simple inscription of these same numbers.
できるだけ、問題の数値データを書き込むことによる誤りの可能性を減らすため、それらはミルの円柱のひとつに連続して置かれる。そして、オペレータが注意を払う必要なく、この目的のために用意されたカードにより、これらの数値は自ら必要な円柱に用意される。それ故、オペレータはこれらの数値を入力することに専心できる。
According to what has now been explained, we see that the collection of columns of Variables may be regarded as a store of numbers, accumulated there by the mill, and which, obeying the orders transmitted to the machine by means of the cards, pass alternately from the mill to the store and from the store to the mill, that they may undergo the transformations demanded by the nature of the calculation to be performed.
何が説明されているのかによって、変数をなす円柱の集まりは、数値を格納するとみなされるであろう。その数値はミルに貯められ、カードによりこの機械に送られた命令に応じて、ミルからストア（store）、ストアからミルへ行き来し、実行される計算の性質によって要求される変化を経る。
Hitherto no mention has been made of the signs in the results, and the machine would be far from perfect were it incapable of expressing and combining amongst each other positive and negative quantities. To accomplish this end, there is, above every column, both of the mill and of the store, a disc, similar to the discs of which the columns themselves consist. According as the digit on this disc is even or uneven, the number inscribed on the corresponding column below it will be considered as positive or negative. This granted, we may, in the following manner, conceive how the signs can be algebraically combined in the machine. When a number is to be transferred from the store to the mill, and vice versa, it will always be transferred with its sign, which will effected by means of the cards, as has been explained in what precedes. Let any two numbers then, on which we are to operate arithmetically, be placed in the mill with their respective signs. Suppose that we are first to add them together;the operation-cards will command the addition:if the two numbers be of the same sign, one of the two will be entirely effaced from where it was inscribed, and will go to add itself on the column which contains the other number;the machine will, during this operation, be able, by means of a certain apparatus, to prevent any movement in the disc of signs which belongs to the column on which the addition is made, and thus the result will remain with the sign which the two given numbers originally had. When two numbers have two different signs, the addition commanded by the card will be changed into a subtraction through the intervention of mechanisms which are brought into play by this very difference of sign. Since the subtraction can only be effected on the larger of the two numbers, it must be arranged that the disc of signs of the larger number shall not move while the smaller of the two numbers is being effaced from its column and subtracted from the other, whence the result will have the sign of this latter, just as in fact it ought to be. The combinations to which algebraical subtraction give rise, are analogous to the preceding. Let us pass on to multiplication. When two numbers to be multiplied are of the same sign, the result is positive;if the signs are different, the product must be negative. In order that the machine may act conformably to this law, we have but to conceive that on the column containing the product of the two given numbers, the digit which indicates the sign of that product has been formed by the mutual addition of the two digits that respectively indicated the signs of the two given numbers;it is then obvious that if the digits of the signs are both even, or both odd, their sum will be an even number, and consequently will express a positive number;but that if, on the contrary, the two digits of the signs are one even and the other odd, their sum will be an odd number, and will consequently express a negative number. In the case of division. instead of adding the digits of the discs, they must be subtracted one from the other, which will produce results analogous to the preceding;that is to say, that if these figures are both even or both uneven, the remainder of this subtraction will be even;and it will be uneven in the contrary case. When I speak of mutually adding or subtracting the numbers expressed by the digits of the signs, I merely mean that one of the sign-discs is made to advance or retrograde a number of divisions equal to that which is expressed by the digit on the other sign-disc. We see, then, from the preceding explanation, that it is possible mechanically to combine the signs of quantities so as to obtain results conformable to those indicated by algebra.
今までは結果の符号について言及しなかった。この機械は、正負の量を結合し表現する能力がなく、これでは決して完璧ではない。これを達成するために、ストアとミル両方の全ての円柱の上に、円柱自身を構成するものと同様の円盤を置く。このディスクの桁が偶数か奇数かによって、下の円柱に書かれた数値はそれぞれ正もしくは負とみなす。これにより、次のやり方で、この機械で符号がどのように算術演算されるかを考えることができる。ストアからミルへ数値が送られた時、もしくはその逆の時、必ず符号も一緒に送られる。それはカードにより実行される。それは先立つことで説明された。我々が計算を行うどんな二つの数値も、それぞれの符号と一緒にミルの中に置くとする。最初にそれを足すならば、演算カードは加算を命令する。二つの数値の符号が同じであれば、そのうちのひとつは完全に書かれている円柱から消去される。そして、もう一方の番号が書かれている円柱に加算される。この処理の間、この機械は、なんらかの装置により、加算が実行される円柱の符号が動くのを制することができる。二つの数値が違う符号を持っていた場合は、まさしくこの符号の違いにより導入される機構の介入によって、カードによって指示された加算命令は減算命令に変更される。減算は二つのうちの大きい方の数値にのみ有効なので、小さい数値がその円柱から消去され、もう一方の数値から減じられる間は、大きい数値の符号を示す円盤は動かない。そこから、ちょうど実際にそうあるべき通り、結果は大きい数字の符号を持つことになる。減算の場合もこれと同様となる。乗算について考える。掛け合わされる二つの数値の符号が同じ場合は結果は正になる。符号が違う場合は積は負になる。この機械がこの規則に従って動作するために、与えられた二つの数値の積を格納する円柱では、積の符号を示す桁は、二つの数字の符号を示す桁の相互的な加算によって作られるとみなさなければならない。符号の桁が両方とも偶数、もしくは奇数だった場合は、その合計数は偶数になり、正の符号を表現する。しかし、対照的に、二つの符号の桁が、一方が偶数でもう一方が奇数の場合、その合計数は奇数になり、負の符号を表現する。除算の場合、符号の桁の円盤の合計の代わりに、一方からもう一方を減算しなければいけない。それは乗算の場合と同様の結果になる。これらの桁が両方とも偶数、もしくは奇数の場合、その差の数字は偶数になる。逆の場合は、その差は奇数になる。符号を表現する数を相互に加算もしくは減算というのは、符号円盤のひとつは刻まれた数字を前進、後退させるように出来ている。そしてそれが、他の符号円盤により表示されるものと同じあるというだけのことだ。この説明から、代数で示されたものに従った結果を得るように、機械的に符号の数を結合することが可能であるというのが分かる。
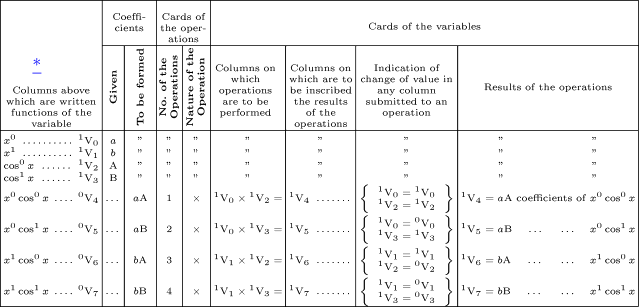
The machine is not only capable of executing those numerical calculations which depend on a given algebraical formula, but it is also fitted for analytical calculations in which there are one or several variables to be considered. It must be assumed that the analytical expression to be operated on can be developed according to powers of the variable, or according to determinate functions of this same variable, such as circular functions, for instance;and similarly for the result that is to be attained. If we then suppose that above the columns of the store, we have inscribed the powers or the functions of the variable, arranged according to whatever is the prescribed law of development, the coefficients of these several terms may be respectively placed on the corresponding column below each. In this manner we shall have a representation of an analytical development;and, supposing the position of the several terms composing it to be invariable, the problem will be reduced to that of calculating their coefficients according to the laws demanded by the nature of the question. In order to make this more clear, we shall take the following very simple example, in which we are to multiply (a + bx1) by (A + B cos1x). We shall begin by writing x0 , x1, cos0x, cos1x, above the columns V0, V1, V2, V3; then since, from the form of the two functions to be combined, the terms which are to compose the products will be of the following nature, x0・cos0x, x0・cos1x, x1・cos0x, x1・cos1x, these will be inscribed above the columns V4, V5, V6, V7. The coefficients of x0, x1, cos0x, cos1x being given, they will, by means of the mill, be passed to the columns V0, V1, V2 and V3. Such are the primitive data of the problem. It is now the business of the machine to work out its solution, that is, to find the coefficients which are to be inscribed on V4, V5, V6, V7. To attain this object, the law of formation of these same coefficients being known, the machine will act through the intervention of the cards, in the manner indicated by the following table:—
この機械は、それらの与えられた代数の公式に従った数値計算を実行する能力だけではなく、ひとつもしくはいくつかの変数を考慮した解析的な計算にも適合している。処理される解析式は、変数や三角関数のような有限関数（determinate functions）の次数に応じて展開することができる。それは得ようとしている結果についても同様である。ストアの円柱の上に、次数もしくは、どのようなものでも、限定された展開規則に従って用意された関数の変数を記すとしよう。それらの項の係数は、対応する円柱に書かれる。この方法により解析展開の表現法を得ることになる。そして、それらの項の位置が不変になるように構成すれば、問題は、その性質により要求される規則に従った係数を計算することに簡易化される。もう少し分かりやすくするために、次の非常に簡単な例、(a + bx1) に (A + B cos1x) を掛けることを取り上げる。円柱 V0、V1、V2、V3 の上に、x0、x1、cos0x、cos1x を書くことから始める。結合される二つの関数の形式から、積の項は次の種類となる。x0・cos0x、x0・cos1x、x1・cos0x、x1・cos1x これらは円柱 V4、V5、V6、V7 の上に記される。係数として x0、x1、cos0x、 cos1x が与えられ、これらはミルにより、V0、V1、V2、V3 に渡される。それらは問題の基本的なデータとなる。ここからがこの機械の仕事である解の計算である。それは V4、V5、V6、V7 に記された係数を見つけることだ。この、これら知られている同じ係数の構成規則という目的に到達するために、この機械は、次の表に示す方法で、カードの仲介により動作する（大きい画像)
It will now be perceived that a general application may be made of the principle developed in the preceding example, to every species of process which it may be proposed to effect on series submitted to calculation. It is sufficient that the law of formation of the coefficients be known, and that this law be inscribed on the cards of the machine, which will then of itself execute all the calculations requisite for arriving at the proposed result. If, for instance, a recurring series were proposed, the law of formation of the coefficients being here uniform, the same operations which must be performed for one of them will be repeated for all the others;there will merely be a change in the locality of the operation, that is, it will be performed with different columns. Generally, since every analytical expression is susceptible of being expressed in a series ordered according to certain functions of the variable, we perceive that the machine will include all analytical calculations which can be definitively reduced to the formation of coefficients according to certain laws, and to the distribution of these with respect to the variables.
いままでの例の中で展開された原理から一般的なアプリケーションへ考察を進める。係数の構成規則が分かれば良いということになる。そして、その規則はこの機械のカードに記される。この機械は、それから、自身で出される結果に至るために必要な全ての計算を実行する。例えば、循環する一連の計算が提示されたとすると、係数の構成規則は一定で、その中のひとつのい、実行しなければいけない、そのなかのひとつである、同じ演算が、他のすべてのために繰り返されることになる。演算の場所が変わるだけで、違う円柱において行われるということだ。通常、あらゆる解析の数式は、ある特定の関数の変数に従った演算の順序によって表現されることを許容するので、この機械は、明らかに、ある規則に従った係数の構成に簡略化できる全ての解析計算を、その範疇に含む。
We may deduce the following important consequence from these explanations, viz. that since the cards only indicate the nature of the operations to be performed, and the columns of Variables with which they are to be executed, these cards will themselves possess all the generality of analysis, of which they are in fact merely a translation. We shall now further examine some of the difficulties which the machine must surmount, if its assimilation to analysis is to be complete. There are certain functions which necessarily change in nature when they pass through zero or infinity, or whose values cannot be admitted when they pass these limits. When such cases present themselves, the machine is able, by means of a bell, to give notice that the passage through zero or infinity is taking place, and it then stops until the attendant has again set it in action for whatever process it may next be desired that it shall perform. If this process has been foreseen, then the machine, instead of ringing, will so dispose itself as to present the new cards which have relation to the operation that is to succeed the passage through zero and infinity. These new cards may follow the first, but may only come into play contingently upon one or other of the two circumstances just mentioned taking place.
これらの説明から次の重要な結論を推論することができるかもしれない。すなわち、カードは実行される演算の性質と、それが実行される変数の円柱を指定するだけなので、これらのカードはそれ自身、解析の大部分を所有することになる。それらは実際のところ単なる翻訳だ。この機械への解析の吸収がなし得たのであれば、それがが克服しなければいけない、いくつかの困難について考えてみる。零もしくは無限大を通る時、もしくは極限を通る時に許容することができない値を通る時には、本質的な変更が必要となる、あるいくつかの関数がある。そのようなケースが与えられた時は、この機械は零や無限大の通過があったことをベルにより警告し、そして、つぎに実行する必要のある何かしらの処理が再びセットされるまでは停止することができる。このエラーが予知されるものならば、この機械は、警鐘を鳴らす代わりに、零と無限大を通過した後の処理に関連した新しいカードを与えるように、自らを配置することになる。これらの新しいカードは最初のものに続くかもしれないが、偶然に、先ほど述べた二つの状態のどちらかになっただけということもあり得る。
Let us consider a term of the form abn; since the cards are but a translation of the analytical formula, their number in this particular case must be the same, whatever be the value of n;that is to say, whatever be the number of multiplications required for elevating b to the nth power (we are supposing for the moment that n is a whole number). Now, since the exponent n indicates that b is to be multiplied n times by itself, and all these operations are of the same nature, it will be sufficient to employ one single operation-card, viz. that which orders the multiplication.
abn という形の項を考える。カードは解析の公式を翻訳したものでもあるから、ある特定のケースにおいてその数値は同じでなければいけない。これをnとする。すなわち、何か、b を n 次の指数に上げるために必要となる乗算の回数である（今は n を自然数とみなす）ここで、指数 n は、b を n 回、自身で乗算することを示している。これられの演算の性質は全て同じでなので、一枚の演算カードを用意するだけで良い。すなわち、乗算のカードである。
But when n is given for the particular case to be calculated, it will be further requisite that the machine limit the number of its multiplications according to the given values. The process may be thus arranged. The three numbers a, b and n will be written on as many distinct columns of the store;we shall designate them V0, V1, V2;the result abn will place itself on the column V3. When the number n has been introduced into the machine, a card will order a certain registering-apparatus to mark (n-1), and will at the same time execute the multiplication of b by b. When this is completed, it will be found that the registering-apparatus has effaced a unit, and that it only marks (n-2);while the machine will now again order the number b written on the column V1 to multiply itself with the product b2 written on the column V3, which will give b3. Another unit is then effaced from the registering-apparatus, and the same processes are continually repeated until it only marks zero. Thus the number bn will be found inscribed on V3, when the machine, pursuing its course of operations, will order the product of bn by a;and the required calculation will have been completed without there being any necessity that the number of operation-cards used should vary with the value of n. If n were negative, the cards, instead of ordering the multiplication of a by bn, would order its division;this we can easily conceive, since every number, being inscribed with its respective sign, is consequently capable of reacting on the nature of the operations to be executed. Finally, if n were fractional, of the form p/q, an additional column would be used for the inscription of q, and the machine would bring into action two sets of processes, one for raising b to the power p, the other for extracting the qth root of the number so obtained.
もし n が、その数の場合を計算するように入力されるのならば、入力される乗算の回数を制限する追加機能を必要とする。その処理は次のように準備されるかもしれない。三つの数字 a、b、n は、それと同数の異なるストアの円柱に書かれる。我々は、それらをV0、V1、V2と称する。結果の abn は V3 に書かれる。この機械に数値 n が入力された時、一枚のカードがある記録装置（registering-apparatus）に (n-1) を記録するよう命令する。そして、そのカードは同時に b と b の乗算を実行する。これが完了すると、記録装置がユニットを消去したのが分かるだろう。そして、新しく (n-2) を記録するだけである。同時に、この機械は再び V1 の円柱に書かれた数値 b に、V3 に書かれた積 b2 を乗じるよう命令する。そして、それは b3 を与える。それから、もうひとつのユニットが記録装置から消去される。そして同じ処理が、記録装置のユニットが零になるまで繰り返される。このようにして、数値 bn は V3 に書かれる。この機械は処理を続け bn に a を乗じるよう命令する。そして、数値 n と同じだけのカード枚数を必要とすることなく、必要な計算は完了することになる。もし、n が負であれば、カードは a に bn を乗じる代わりに、割るように命じることになる。これは簡単に分かることだ。なぜならば、対応して符号付けされた数はどれもみな、実行する演算の性質に作用することができるからだ。最後に、n が p/q という形の小数の場合は、ひとつ余分な円柱を使って q を書き込む、そして、機械は二組の処理を行うことになる。ひとつは b の p 乗、もうひとつはそれで得られた数の q 乗根である。
Again, it may be required, for example, to multiply an expression of the form axm+bxn by another Axp+Bxq, and then to reduce the product to the least number of terms, if any of the indices are equal. The two factors being ordered with respect to x, the general result of the multiplication would be Aaxm+p+Abxn+p+Baxm+q+Bbxn+q. Up to this point the process presents no difficulties;but suppose that we have m=p and n=q, and that we wish to reduce the two middle terms to a single one (Ab+Ba)xm+q. For this purpose, the cards may order m+q and n+p to be transferred into the mill, and there subtracted one from the other;if the remainder is nothing, as would be the case on the present hypothesis, the mill will order other cards to bring to it the coefficients Ab and Ba, that it may add them together and give them in this state as a coefficient for the single term xn+p=xm+q.
再び、axm+bxn に Axp+Bxq を乗じて、もし全ての指数が同じならば、積を最小の項数に減じることの例を示す必要があるだろう。二つの要素を x により順番付けると、その乗算の一般的な結果は Aaxm+p+Abxn+p+Baxm+q+Bbxn+q となる。ここまでの処理に難しいところは無い。しかし、m=p と n=q という条件があるとする。この時、中心の二項を一つにまとめたいと (Ab+Ba)xm+q 思うだろう。この目的のために、カードは m+q と n+p をミルに送り、そこで一方からもう一方を減じるよう命令するだろう。現在の仮定のように、減算の結果が零ならば、ミルは別のカードに係数 Ab と Ba を持ってくるよう指示する。そして足し合わせて、単一の項 xn+p=xm+q の係数にするだろう。
This example illustrates how the cards are able to reproduce all the operations which intellect performs in order to attain a determinate result, if these operations are themselves capable of being precisely defined.
この例は、正確に意味するところが分かる演算であれば、カードがどのようにして、限定された結果に出す代わりに、全ての演算で知性を発揮するかを示すものだ。
Let us now examine the following expression:—
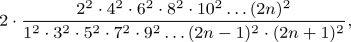
which we know becomes equal to the ratio of the circumference to the diameter, when n is infinite. We may require the machine not only to perform the calculation of this fractional expression, but further to give indication as soon as the value becomes identical with that of the ratio of the circumference to the diameter when n is infinite, a case in which the computation would be impossible. Observe that we should thus require of the machine to interpret a result not of itself evident, and that this is not amongst its attributes, since it is no thinking being. Nevertheless, when the cos of n =1/0 has been foreseen, a card may immediately order the substitution of the value of π (π being the ratio of the circumference to the diameter), without going through the series of calculations indicated. This would merely require that the machine contain a special card, whose office it should be to place the number π in a direct and independent manner on the column indicated to it. And here we should introduce the mention of a third species of cards, which may be called cards of numbers. There are certain numbers, such as those expressing the ratio of the circumference to the diameter, the Numbers of Bernoulli, &c., which frequently present themselves in calculations. To avoid the necessity for computing them every time they have to be used, certain cards may be combined specially in order to give these numbers ready made into the mill, whence they afterwards go and place themselves on those columns of the store that are destined for them. Through this means the machine will be susceptible of those simplifications afforded by the use of numerical tables. It would be equally possible to introduce, by means of these cards, the logarithms of numbers;
but perhaps it might not be in this case either the shortest or the most appropriate method;
for the machine might be able to perform the same calculations by other more expeditious combinations, founded on the rapidity with which it executes the first four operations of arithmetic.
To give an idea of this rapidity, we need only mention that Mr. Babbage believes he can, by his engine, form the product of two numbers, each containing twenty figures, in three minutes.
ここで次の式について考える。
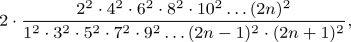
n が無限大になると、この式が円周率と等しくなることは自明だ。
ここで我々はこの機械に、この分数式を計算するだけではなく、さらに進んで円周率と同一とみなせるになったと同時に知らせることを要求するだろう。実際に n が無限大のケースというのは計算できないのだ。これを調べるには、この機械が明らかに自身から出たものではない結果について解釈するよう要求しなければいけない。この機械は思考する存在ではないので、これは得意とするところではない。それでも、n = 1/0 の時の cos は見通すことができて (?)、指示された一連の計算を行うことなく、カードはそれをπ（πは円周率）に置き換えるよう命じるだろう。これはこの機械に特別なカードを置くだけで良い。そこでは、πが直接かつ独立した方法で円柱に書かれている。ここで、我々は三種類目のカードについて言及しなければいけない。それは定数のカードと呼ばれるべきものである。ベルヌイ数や円周率のように度々計算に用いられる決まった定数がある。それを使う度に毎回計算する必要が無いように、これらを既成の数値とするために、あるいくつかのカードをミルに特別に組み込んでおくことができるだろう。これにより、カードはそのためのストアの円柱に、それ自身に記された定数として書き込まれる。この手段によって、この機械は定数表を使用することにより得られる簡略化を許すことになる。これは、これらのカードによって対数表を使うことができることを意味するだろう。しかし、もしかするとそれは、この場合もっとも最短、もしくは最適な方法ではないかもしれない。この機械は、四則演算を実行するところの速さに依存した、より迅速な組み合わせにより、同じ計算を実行できるかもしれないからだ。この速さについては、バベッジ氏が彼の機関によって、三分以内に十二桁の数値の乗算ができると信じている、としか言えない。
※ この無限乗積による円周率の計算はイギリスのウォリスが発見したもの。
Perhaps the immense number of cards required for the solution of any rather complicated problem may appear to be an obstacle;but this does not seem to be the case. There is no limit to the number of cards that can he used. Certain stuffs require for their fabrication not less than twenty thousand cards, and we may unquestionably far exceed even this quantity.
おそらく、少しでも複雑な問題の解決のためには、必要なカードの莫大な数が障害であるように見えるかもしれない。しかし、これはそうではない。使用できるカードの枚数には制限はない。ある計算はそれを成すのに二万枚をくだらないカードを必要とする場合がある。そして、疑いなくこの枚数をはるかに上回ることもあり得る。
Resuming what we have explained concerning the Analytical Engine, we may conclude that it is based on two principles: the first consisting in the fact that every arithmetical calculation ultimately depends on four principal operations&addition, subtraction, multiplication, and division; the second, in the possibility of reducing every analytical calculation to that of the coefficients for the several terms of a series. If this last principle be true, all the operations of analysis come within the domain of the engine. To take another point of view: the use of the cards offers a generality equal to that of algebraical formula, since such a formula simply indicates the nature and order of the operations requisite for arriving at a certain definite result, and similarly the cards merely command the engine to perform these same operations; but in order that the mechanisms may be able to act to any purpose, the numerical data of the problem must in every particular case be introduced. Thus the same series of cards will serve for all questions whose sameness of nature is such as to require nothing altered excepting the numerical data. In this light the cards are merely a translation of algebraical formula, or, to express it better, another form of analytical notation.
今まで解析機関について説明していたものに再び戻ると、それは二つの原則に基づくと結論づけることができるだろう。最初の原則は、あらゆる数値計算が最終的には、加算、減算、乗算、除算という四つの演算によりなされるという事実である。二番目の原則は、あらゆる解析計算は、級数のそれぞれの項の係数の計算に簡略化できる可能性があるということである。最後の原則が真実ならば、全ての解析処理はこの機関によってできるということになる。別の見方をすると、カードの使用は代数の公式を使うことである。なぜならば、そのような公式は確実な結果に至るために必要な演算の命令と性質を単に示すものだからである。カードはそれと同じように機関に演算を命令するにすぎない。しかし、機構をいかなる目的にも供することができるようにするために、どのような場合であっても、問題の数値データは入力されなければいけない。数値データを変更する以外は要求しないような単調さを持つ問題は、全て同じ一連のカードにより処理されることになる。このような観点からも、カードは単に代数公式を翻訳したもの、もしくはそれをより良く、解析的な表記の形で表現したものなのだ。
Since the engine has a mode of acting peculiar to itself, it will in every particular case be necessary to arrange the series of calculations conformably to the means which the machine possesses; for such or such a process which might be very easy for a calculator may be long and complicated for the engine, and vice versa.
この機関はそれ特有の動作モードを持つので、どのような場合でも、この機械のやり方に応じた一連の計算を用意する必要がある。計算手にとってはとても簡単なものが、この機関には長く複雑なものになることもある、そしてその逆の場合もあり得る。
Considered under the most general point of view, the essential object of the machine being to calculate, according to the laws dictated to it, the values of numerical coefficients which it is then to distribute appropriately on the columns which represent the variables, it follows that the interpretation of formula and of results is beyond its province, unless indeed this very interpretation be itself susceptible of expression by means of the symbols which the machine employs. Thus, although it is not itself the being that reflects, it may yet be considered as the being which executes the conceptions of intelligence. The cards receive the impress of these conceptions, and transmit to the various trains of mechanism composing the engine the orders necessary for their action. When once the engine shall have been constructed, the difficulty will be reduced to the making out of the cards; but as these are merely the translation of algebraical formula, it will, by means of some simple notations, be easy to consign the execution of them to a workman. Thus the whole intellectual labour will be limited to the preparation of the formula, which must be adapted for calculation by the engine.
ごく一般的な視点から考えると、この機械の最も重要な目的は、指示された規則に従い変数を表現する円柱に適切に分配された係数の値を計算することであろう。実際、まさにこの解釈それ自身がこの機械が使用する記号による表現を許容するようにならない限りは、この機械は公式と結果の解釈がそれ自身の領域を超えたということに追従する。この機械は、それ自身考える存在ではないが、それでも、思考による方針に従い行動する存在のようにみなすことも出来るだろう。カードはこのような方針を刻印させるためのもので、この機関を構成する機構に、それらを稼働させるのに必要な命令を伝える。一度このような機関が構築されると、困難はカードを作成するだけということになる。とは言っても、台数公式を翻訳するだけのことなので、いくつかの単純な表記によって、運用者にそれの実行を委託するのは簡単なことだろう。従って、知性を必要とする作業の全体は、その機関で計算するのに適した形で、公式を表現することに限られる。
Now, admitting that such an engine can be constructed, it may be inquired: what will be its utility? To recapitulate; it will afford the following advantages:‐First, rigid accuracy. We know that numerical calculations are generally the stumbling-block to the solution of problems, since errors easily creep into them, and it is by no means always easy to detect these errors. Now the engine, by the very nature of its mode of acting, which requires no human intervention during the course of its operations, presents every species of security under the head of correctness: besides, it carries with it its own check; for at the end of every operation it prints off, not only the results, but likewise the numerical data of the question; so that it is easy to verify whether the question has been correctly proposed. Secondly, economy of time: to convince ourselves of this, we need only recollect that the multiplication of two numbers, consisting each of twenty figures, requires at the very utmost three minutes. Likewise, when a long series of identical computations is to be performed, such as those required for the formation of numerical tables, the machine can be brought into play so as to give several results at the same time, which will greatly abridge the whole amount of the processes. Thirdly, economy of intelligence: a simple arithmetical computation requires to be performed by a person possessing some capacity; and when we pass to more complicated calculations, and wish to use algebraical formula in particular cases, knowledge must be possessed which presupposes preliminary mathematical studies of some extent. Now the engine, from its capability of performing by itself all these purely material operations, spares intellectual labour, which may be more profitably employed. Thus the engine may be considered as a real manufactory of figures, which will lend its aid to those many useful sciences and arts that depend on numbers. Again, who can foresee the consequences of such an invention? In truth, how many precious observations remain practically barren for the progress of the sciences, because there are not powers sufficient for computing the results! And what discouragement does the perspective of a long and arid computation cast into the mind of a man of genius, who demands time exclusively for meditation, and who beholds it snatched from him by the material routine of operations! Yet it is by the laborious route of analysis that he must reach truth; but he cannot pursue this unless guided by numbers; for without numbers it is not given us to raise the veil which envelopes the mysteries of nature. Thus the idea of constructing an apparatus capable of aiding human weakness in such researches, is a conception which, being realized, would mark a glorious epoch in the history of the sciences. The plans have been arranged for all the various parts, and for all the wheel-work, which compose this immense apparatus, and their action studied; but these have not yet been fully combined together in the drawings and mechanical notation. The confidence which the genius of Mr. Babbage must inspire, affords legitimate ground for hope that this enterprise will be crowned with success; and while we render homage to the intelligence which directs it, let us breathe aspirations for the accomplishment of such an undertaking.
さて、そのような機関が構築できるとして、次のような問いがあるだろう。その有用性は何か？要約すると以下の利点がある。まず、厳正な正確さ。数値計算は問題を解決する上での障害であることが分かる。簡単に誤りが入り込むし、それを検知するのは決して簡単ではない。この機関であれば、その動作形態の性質から、演算の過程で人の介入を必要としないし、題目である正確性によりあらゆる種類の安全を提供する。それに加えて、機関に自身のチェック機能もある。機関は、演算が終わる度に、結果だけではなく問題の数値データも出力する。従って、問題が正しく与えられたか確認するのが簡単である。第二番目は、時間の節約である。これを確かめるために、我々は三分以内に十二桁の数値の乗算ができることを思い出さなくてはいけない。同じように、数値表の構成長い一連の同じ計算が実行される場合、この機械は、同時にいくつかの結果を与えるように動くことができる。それは、大量の処理全体をかなり短い時間で終えることにつながる。第三に知性の節約である。単純計算は若干の能力を備えている人によってされることを要求する。より複雑な計算の場合は、ある場合は台数公式を使うことを望むだろう。そのような場合は、若干の範囲の予備数学的な研究を前提とする知識は備えられていなければいけない。さて、この機関の場合は、純粋な演算そのものはそれ自身でこなす能力があるので、人が行う方がより有用なものとして、知性的な作業を残す。従って、機関は真に数字の工場と見なせる。それは、多くの数字に依存する科学や技術に役に立つだろう。再び問いに戻る。誰がそのような発明の結果を予知することができるだろうか？実際、いくつの貴重な研究が、結果を計算する力の不足により、実質的に科学の進歩にとって不毛な状態で残されていることだろう。何が、本当は深い思考にだけ時間を使いたいと思っている天才の心に投げかけられた長くつまらない計算に関する釣り合いのとれた見方を押し阻んでいるのだろうか。そして、誰かが、実際に決まり切った手順による計算が、彼からそれを奪っていることに気付いているのだろうか。とはいえ、真実に到達することは、面倒な解析の積み重ねなのだ。数によって導かれない限り、彼はこれを追い続けることができない。数字なしに、自然の謎を覆うベールを上げることはできない。従って、そのような研究における人間の弱点を補う能力を持つ装置を組み立てるという考えは、現実的になりつつあるし、科学の歴史の中に素晴らしい一時代を築くだろう。この計画は様々な分野にわたっている。そしてそれが、この巨大な装置とその研究された動作を作り出すのだ。しかし、これらはまだ完全な機械的な表現による設計に落とし込まれていない。バベッジ氏の才能に触発された自信は、この事業が成功を授けられるという望みの妥当な根拠の持っている。そのようなことを指揮する知性に敬意を払うと同時に、そのような考えを実現するという大きな望みをもとうではないか。